
Figure 1
Logo du LNE.

Figure 2
Salle des machines pour la climatisation.

Figure 3
Photographie des massifs gravimétrie et balance du watt en béton armé lors de leur construction en 2003.

Figure 4
Photographie du blindage des salles par métallisation continue des parois et des sols (les portes sont intégrées dans ces blindages
et munies pour cela de contacts électriques sur leur pourtour et d'une vitre finement grillagée.
Un nouveau bâtiment au LNE
La conception et la construction d'un nouveau bâtiment sur le site LNE de Trappes (figure 1) s'est étendue de 2002 à 2004. Le bâtiment destiné à abriter les
laboratoires de métrologie électrique fondamentale et de nanométrologie, a une emprise au sol de 56 m x 57 m, auxquels s'ajoute une avancée de 9 m
utilisée pour l'accueil et les salles de réunion. Au total, l'emprise au sol atteint 3 380 m².
Le bâtiment est divisé en trois parties:
- Un local technique de 1016 m² destiné à recevoir les installations de climatisation (figure 2), le transformateur d'alimentation électrique général, un
onduleur, la chaufferie et le groupe de réfrigération.
- Une zone de laboratoires et une aire de stockage et de maintenance de 1 660 m² au total. Cette zone comprend: (1) 8 laboratoires de métrologie
électrique dont la superficie est comprise entre 20 et 60 m² (étalon de Lampard, métrologie quantique, métrologie basses-fréquences) auxquels sont
associées 7 salles de contrôle de 23 m² environ chacune, (2) un laboratoire de 170 m² comprenant 3 salles pour la balance du watt, la gravimétrie,
l'instrumentation et une salle de contrôle, (3) un laboratoire 110 m² environ, comprenant deux salles de mesure pour les activités de nano-métrologie,
une salle de contrôle commune et une salle de préparation des échantillons, (4) deux salles de préparation et de stockage d'environ 45 m² chacune,
respectivement pour les activités de nano-métrologie et de métrologie électrique.
- Une zone de 110 m² répartie sur deux étages, utilisée pour 22 bureaux de 11 m² environ, les sanitaires prévues pour plus de 30 personnes, les
salles de réunion, l'accueil, la bibliothèque, les couloirs...
De fortes exigences d'environnement
Une attention particulière a été portée à la prise en compte des contraintes environnementales imposées par les dispositifs de mesures vibrations, température, humidité, propreté, gravimétrie...) et celle imposées par le site retenu (vibrations, nature des sols...). Des précautions sont également prises pour s'affranchir des vibrations qui sont générées tant par l'activité interne du bâtiment (couloirs suspendus sur boîte à ressort, implantation des groupes de climatisation sur dalle séparée, dalles indépendantes pour chaque activité) que par l'activité externe (choix de la meilleure implantation en fonction des relevés de vibration effectués sur le site).
Contrôles de la température et de l'hygrométrie
Les locaux dévolus à la balance du watt et au laboratoire de gravimétrie comportent quatre pièces d'une surface totale de 160 m². Elles sont dotées d'un dispositif de contrôle des conditions d'environnement (température et humidité relative). Les désignations, spécifications et usages de chacune des salles sont les suivantes:
- Salle de contrôle: 35 m², (20±0,5)°C. Cette salle joue à la fois le rôle de sas, de salle de rangement et de montage;
- Salle d'instrumentation, destinée à abriter les équipements de mesure sensibles et l'informatique pilotant la manipulation: 35 m², (20±0,1)°C,
(50±5)% HR;
- Salle blanche (salle où se situe la balance du watt): 40 m², (20±0,1)°C, (50±5)% HR, classe 1000.
Atténuation des vibrations
Deux sondages destinés à caractériser l’état hydrogéologique du sous-sol sont disponibles : le premier est un puits de 7 m de profondeur situé dans
le local technique des pompes à l’arrière de la salle de la balance du watt. Le deuxième est un puit extérieur de 45 m de profondeur équipé d’une
sonde piézométrique afin de suivre l’évolution de la nappe phréatique des sables de Fontainebleau, située à - 33 m.
Les deux salles, balance du watt et gravimétrie, comportent deux massifs symétriques en béton (figure 3) (6 m×5,5 m, épaisseur 2 m,
pour une masse de 150 tonnes), isolés des dalles et murs des bâtiments et supportés chacun par quatre piliers de 12 m de longueur, ancrés dans les
couches stables du sous-sol, garantissant une sensibilité minimale aux vibrations et l’assurance d’une horizontalité très stable. Pour ces salles,
l’option d’une récupération de l’air par le plancher, supposant une géométrie de dalle complexe, avec pour conséquence des inhomogénéité de l’accélération
de la pesanteur g a été abandonnée au profit d’une récupération latérale au niveau du sol permettant de bénéficier d’une structure de dalle homogène
minimisant les variations spatiales de g.
Des précautions sont également prises pour s’affranchir des vibrations qui sont générées tant par l’activité interne du bâtiment (couloirs suspendus
sur boîtes à ressort, implantation des groupes de climatisation sur dalle séparée, dalles indépendantes pour chaque activité) que par l’activité
externe (choix de la meilleure implantation en fonction des relevés de vibration effectués sur le site).
Blindage électrique
La salle blanche et celle des appareils de mesure sont installées à l’intérieur d’une cage de Faraday (figure 4) (atténuation de 40 dB à 60 dB de 1 MHz à quelques GHz).

Figure 1
Schéma de principe de la phase statique.

Figure 2
Schéma de principe de la phase dynamique.
Principe de la mesure
L'expérience consiste à effectuer la comparaison d'une puissance mécanique à une puissance électromagnétique (d'où son nom). Elle résulte d'une mesure effectuée en deux étapes: une phase statique, au cours de laquelle la force électromagnétique (force de Laplace) s'exerçant sur un conducteur parcouru par un courant et placé dans un champ d'induction est comparée au poids d'une masse étalon, et une phase dynamique où l'on détermine la tension induite aux bornes du même conducteur lorsqu'il est déplacé dans le même champ d'induction avec vitesse connue.
Phase statique
Au cours de la phase statique (figure 1), on équilibre le poids d’une masse étalon mg et d’une force électromagnétique nominalement verticale F en imposant la circulation d’un courant I dans une bobine de longueur l plongée dans un champ d’induction magnétique B:

Phase dynamique
Au cours de la phase dynamique (figure 2), le même conducteur est déplacé dans le même champ d'induction avec une vitesse verticale vz. Une tension
induite U (égale à la variation du flux coupé pendant le déplacement) apparaît alors aux bornes de la bobine:
 La phase dynamique constitue une détermination indirecte du produit Bl.
La phase dynamique constitue une détermination indirecte du produit Bl.
La combinaison des relations décrivant les phases statique et dynamique conduit alors à une relation qui exprime l'équivalence entre puissance mécanique et puissance électrique (d'où le nom de balance du watt)

En pratique, le courant I est déterminé par la loi d'Ohm en mesurant la chute de potentiel V qu'il provoque aux bornes d'une résistance R.
Comment établir une relation entre la masse m et la constante de Planck h ?
Deux effets quantiques macroscopiques, issus de la physique du solide, sont actuellement couramment utilisés dans les laboratoires nationaux de
métrologie pour assurer la conservation du volt et de l'ohm avec des incertitudes relatives de l'ordre de 10-9.
L'effet Josephson permet de générer des tensions quantifiées aux bornes de jonctions supraconducteur- isolant-supraconducteur soumises à un
rayonnement hyperfréquence de fréquence f. Une jonction Josephson est un convertisseur fréquence tension (U=f/KJ) dont le coefficient de
proportionnalité KJ (constante Josephson) s'exprime en fonction de la charge de l'électron e et de la constante de Planck h
(KJ=2e/h).
De façon similaire, l'effet Hall quantique (quantification de la résistance de Hall d'un gaz d'électrons bi-dimensionnel, souvent obtenu à basse
température dans des hétérostructures à l'arséniure de gallium) fixe des valeurs de résistance proportionnelles au quantum de
résistance RK (constante de von Klitzing, RK=h/e²).
La détermination des valeurs des tensions U et de la résistance R par comparaison à l'effet Josephson et à l'effet Hall quantique permet
d'exprimer la valeur de la masse m en fonction d'une combinaison des constantes KJ et RK indépendante de la charge de l'électron.
On obtient:
 où A est un paramètre connu contenant les fréquences d’irradiation hyperfréquence et les indices de marche des réseaux Josephson
ainsi que l’indice du plateau de quantification de résistance.
où A est un paramètre connu contenant les fréquences d’irradiation hyperfréquence et les indices de marche des réseaux Josephson
ainsi que l’indice du plateau de quantification de résistance.

Figure 1
Photographie d’ensemble de la balance du watt du LNE.
Repère 1 : dispositif de guidage.
Repère 2 : bobine et comparateur de forces.

Figure 2
Schéma CAO et photographie du système de translation à lames flexibles.
La dimension d’ensemble du système est d’environ 700 mm×700 mm×900 mm.
La partie mobile est présentée à la position où les articulations flexibles ne sont pas déformées.

Figure 3
Schéma CAO du fléau.

Figure 4
Schéma du comparateur de forces : fléau et suspensions.
Le comparateur de forces supporte à son extrémité gauche la suspension de tare à deux
segments. À son extrémité droite, il supporte la suspension à deux segments de la bobine, ainsi que la suspension à deux segments de la masse étalon.
Ces deux suspensions sont reliées par le double-cardan électro-usiné.
Notez que :
1) l’axe x est horizontal et parallèle à l’axe longitudinal du fléau,
2) l’axe y qui plonge dans le plan de la figure est horizontal et perpendiculaire à l’axe x
3) l’axe z est vertical et ascendant.

Figure 5
Photographie du double cardan en situation.

Figure 6
Photographie du circuit magnétique.

Figure 7
Coupe radiale du circuit magnétique. Pour une meilleure lisibilité, certaines arêtes sont cachées. L’entrefer utile est le volume
de forme torique délimité par deux surfaces cylindriques appartenant respectivement au pôle intérieur et au pôle extérieur. Le diamètre extérieur
et la hauteur du circuit sont respectivement égaux à 550 mm et 200 mm. La masse totale est de l’ordre de 350 kg.


Figure 8
Mesures de l’intensité du champ magnétique dans l’axe de révolution du circuit magnétique, d’une altitude de 9 cm au-dessus
de sa face supérieure, jusqu’à une altitude de 46,1 cm. Le cartouche présente l’agrandissement de la zone où se trouve la masse étalon.

Figure 9
Vue CAO de l'échangeur de masse.


Figure 10
Gravimètre absolu associé à la balance du watt
Dispositif de guidage
Objet
Durant la phase dynamique, le comparateur de forces (fléau et ses suspensions) est déplacé d’un seul bloc au moyen d’un dispositif de guidage
actionné par un moteur pas à pas, de façon à ne pas utiliser le fléau comme élément générateur de mouvement.
Le déplacement vertical des plateaux mobiles (assuré par le système de guidage) est asservi, mais le mouvement global doit néanmoins être aussi
régulier que possible. Les discontinuités de la force de commande, provoquées par exemple par le jeu et la friction des roulements, doivent être
évitées. De plus, le guidage à longue course doit être compatible vide et amagnétique afin de perturber au minimum la densité de flux magnétique
dans lequel la bobine est placée. La solution retenue est d’utiliser des articulations flexibles : la variation de la force de pilotage est bien
contrôlée car elle varie continûment comme une fonction de la déformation élastique des articulations.
De plus, ce système est compatible vide et peut être réalisé à l’aide de matériaux non magnétiques.
Description
Le dispositif de guidage repose sur l’utilisation de pivots à lames flexibles. Il comprend des parties fixes et mobiles constituées de deux plateaux
parallèles reliés entre eux par des octopodes.
Sa partie mobile est reliée à la partie fixe au moyen de six jambes comportant chacune trois articulations qui contraignent le mouvement selon un seul
degré de liberté (repère 1 de la figure 1 et figure 2) : chacune des trois paires de jambes est placée à 90° de la précédente (la disposition n’est donc pas symétrique). Chaque
articulation comprend quatre lames flexibles perpendiculaires deux-à-deux. Cet arrangement en lames croisées permet d’augmenter la raideur transverse
du système de translation.
L’ajustement du parallélisme des axes de rotation des pivots permet de réduire les non-linéarités et les rotations parasites du mouvement à des valeurs
inférieures à 1 μm et 5 μrad pour une trajectoire utile de l’ordre de 40 mm (le reste de la trajectoire, pour une totalité de 75 mm, est utilisé
pour l’accélération et la décélération de la bobine). Le positionnement de l’ensemble du dispositif de guidage sur la structure support du dispositif
expérimental, contrôlé avec un inclinomètre, permet d’obtenir cette condition avec une incertitude de quelques microradians.
Tous les éléments du système de translation sont composés d’alliage d’aluminium à l’exception des lames flexibles faites d’un alliage de cuivre et de la
visserie en titane.
Bien que le système de translation supporte une masse totale d’environ 15 kg, et qu’il faille déformer les lames flexibles pour le déplacer, un système
de compensation à contrepoids par jambe flexible permet de réduire la force nécessaire au déplacement de 150 N à moins de 10 N.
Moteur
Pour déplacer le système de translation, un moteur pas-à-pas commercial (Aerotech) à longue course (100 mm) est utilisé. Il est contrôlé par sa propre
boucle d’asservissement sur un codeur linéaire (gravé au pas de 4 μm et interpolé 1000 fois) solidaire du système de translation.
La partie mobile du système de translation est ainsi actionnée par une platine à vis sans fin dont la base est faite d’alliage d’aluminium. L’écrou de la
vis sans fin et les guidages linéaires de la platine sont faits d’acier.
Comparateur de forces
Le comparateur de forces est constitué d’un fléau et de ses suspensions supportant notamment la masse étalon et la bobine. Il est fixé à la partie inférieure du système de guidage.
Fléau
Le fléau du comparateur de forces (figure 3), développé spécifiquement pour l’expérience, est symétrique et à lames flexibles. Ses deux bras (longueur L1 et L2) mesurent chacun 100 mm de long pour une masse d’environ 200 g. Les 3 pivots sont constitués de lames flexibles pincées en acier inoxydable de 20 μm d’épaisseur, pour une largeur de 2 cm. La position angulaire du fléau (inclinaison relative par rapport à l’horizontale) est asservie durant la pesée au moyen d’un capteur optique dont la gamme est ajustée à environ 30 μm.
Suspensions
Ce fléau supporte d’un côté une suspension de tare et de l’autre une double suspension (figure 4). Cette double suspension est constituée d’une part de la
suspension destinée à la masse étalon (masse nominale de 500 g) et d’autre part de la suspension de la bobine.
Une attention particulière a été portée à la réduction des effets de désalignements et des couplages statiques et dynamiques, notamment par
l’utilisation de pivots.
- À l’extrémité du fléau qui soutient la suspension bobine et la suspension de masse, s’exercent deux forces qui doivent être comparées. Pour
assurer à la force gravitationnelle (s’exerçant sur la masse étalon) et à la force de Laplace (s’exerçant sur la bobine) le même point d’application,
les deux suspensions sont reliées par un double cardan monolithique usiné par électroérosion (figure 5). Constituées de sections rigides, elles sont articulées
chacune en leur milieu par un cardan à lames pincées permettant entre autre de minimiser les effets de décentrage de la masse étalon et de réduire
les moments parasites exercés sur le fléau (du fait de la faible raideur angulaire des cardans). Par ailleurs, ’autocentrage de la masse étalon dans
la suspension masse est assurée.
- À l’extrémité du fléau qui soutient la suspension de tare, un contrepoids compense à quelques milligrammes près le moment des forces
exercées de l’autre côté de la suspension par les poids morts, telle le poids de la bobine. Cette suspension est également articulée en son milieu
afin de symétriser aussi parfaitement que possible le comparateur de forces.
La suspension de bobine est donc articulée au moyen de trois pivots (deux cardans et une lame flexible d’extrémité), ce qui permet de distinguer les
forces horizontales des moments qui s’exercent sur la bobine en mesurant la déviation angulaire des deux segments de la suspension par rapport à
leur position d’équilibre à courant nul. En pratique, on mesure la position et l’inclinaison de la bobine pour obtenir la déviation angulaire des
segments.
Circuit magnétique et bobine
Les caractéristiques du circuit magnétique et de la bobine ont été définies de façon à obtenir une tension V de 1 V pour la phase statique et une fem U de 1 V avec pour la phase dynamique. En effet, la mesure d’une tension de 1 V à l’aide de réseau programmable de Josephson est particulièrement bien maîtrisée. Toutefois, l’utilisation d’aimants permanents pour le circuit magnétique le rend sensible aux variations de température, les courants circulant dans la bobine doivent être limités à quelques milliampères en phase statique. Équilibrer la moitié du poids de la masse étalon dans ces conditions oblige, à moins d’utiliser une bobine de très grande longueur de fil (qui annulerait du fait de sa résistance, l’avantage que confèrent les faible courants vis à vis de l’effet Joule), à disposer d’une induction magnétique de forte amplitude. Ainsi, il a été décidé de concevoir un circuit magnétique permettant de disposer d’un champ radial de valeur nominale 1 T, et d’utiliser la bobine décrite ci-dessous. Alors, la vitesse de translation vz de la phase dynamique est de 2 mm/s pour obtenir aux bornes de la bobine une fem de 1 V.
Bobine
L’ensemble bobine – circuit magnétique a donc été conçu de façon à pouvoir générer une force suffisante pour équilibrer la moitié du poids de la
masse étalon sans générer de dégagement de chaleur rédhibitoire dans le circuit magnétique.
La bobine est composée de 580 m de fil de cuivre enroulé en 8 couches concentriques de 22 mm de haut et de 86 tours sur un support en Delrin
d’un diamètre moyen de 268 mm. Le fil de cuivre, isolé par 15 μm de polyesteramide THEIC a un diamètre de 250 μm et sa résistance est de
170 Ω. Cette configuration limite la puissance dégagée par le courant de 5 mA parcourant la bobine à quelques 5 mW, réduisant ainsi l’influence du
coefficient de température du samarium-cobalt du circui magéntique sur la valeur du champ d’induction.
Circuit magnétique
a. Objet
Les premières modélisations par la méthode des éléments finis ont permis de déterminer les caractéristiques géométriques du circuit magnétique
nécessaire à la génération d’un champ radial de 1 T dans un entrefer dont le diamètre moyen est égal à 27 cm. Ce dernier permet un déplacement utile
de la bobine de 40 mm.
Par ailleurs, le champ doit présenter au milieu de l’entrefer un minimum qui définit l’endroit où sera placée la bobine en
phase statique, de façon à diminuer la sensibilité aux erreurs de positionnement verticaux de cette dernière. Le profil obtenu présente en effet
un minimum relatif de l’ordre de 1×10-4 au milieu de la profondeur de l’entrefer.
En phase dynamique, la variation de champ d’induction correspond à 100 μV induits aux bornes de la bobine, soit une variation de tension inférieure
à une marche de tension Josephson (140 μV).
b. Constitution
Le circuit magnétique (figures 6 et 7), de type aimant de haut-parleur, est constitué :
- D’une couronne de 60 aimants permanents samarium-cobalt Sm2Co17 insérée entre deux anneaux de maintien en fer XC48,
- D’un pôle magnétique extérieur en fer pur (Armco) qui constitue la face externe de l’entrefer;
- Du pôle magnétique intérieur en fer pur qui constitue la face interne de l’entrefer. Cette pièce comporte en son centre un noyau d’alliage
fer-cobalt dont l’induction à saturation atteint 2,38 T. Le noyau est percé lui-même en son centre (diamètre 30 mm);
- Et d’une bague de positionnement (calibre en aluminium) qui permet de positionner les pôles l’un par rapport à l’autre.
La géométrie des pôles magnétiques a été spécialement conçue pour concentrer le champ magnétique dans l’entrefer (champ d’induction radial
de l’ordre de 0,94 T) : on obtient un profil en selle de cheval le long de la direction verticale dans cet entrefer circulaire de diamètre moyen de 27 cm et
de hauteur 9 cm.
Le circuit magnétique supporte par ailleurs la structure à laquelle seront fixés trois interféromètres et trois capteurs de position.
c. Caractérisation
Des expériences ont été réalisées, avant le positionnement de l’aimant dans la balance, au moyen d’un capteur à effet Hall adapté
pour mesurer le profil du champ magnétique dans l’entrefer du circuit magnétique. La sensibilité de la sonde, de l’ordre de 1×10-5 T est suffisante
pour mesurer l’homogénéité spatiale du champ qui est supposée être de l’ordre de 1×10-4 T.
Par ailleurs, une machine tournante spécialement conçue a été utilisée pour mesurer :
- La géométrie de l’entrefer à l’aide de capteurs capacitifs ;
- L’intensité du champ magnétique à l’aide d’une sonde à effet Hall ;
- La direction du champ magnétique à l’aide d’un capteur à effet Faraday.
Ces mesures ex-situ, en utilisant la face supérieure de l’aimant comme référence, ont permis durant le montage de l’aimant dans la balance du watt, d’aligner le plan de son champ magnétique radial sur l’horizontale avec une incertitude de 10 μrad.
d. Dépendance en température
Le samarium-cobalt utilisé dans les aimants permanents du circuit magnétique, qui présente l’avantage de générer une forte et permanente
induction magnétique dans l’entrefer, est sensible aux variations de température. Cette dépendance en température s’exprime par:

où ΔB est la variation de l’induction magnétique B associée au changement de température ΔT, et est environ égale à -3×10-4 K-1. À une variation de température des aimants aussi petite que le millikelvin correspond une variation relative de l’induction magnétique de -3×10-7 K-1. Il n’est donc pas possible de s’affranchir des variations de température de l’aimant sur des durées longues : une méthode d’interpolation, en alternant les phases statiques et les phases dynamiques, sera utilisée.
e. Champ magnétique de fuite
L’induction magnétique dans l’entrefer du circuit magnétique est de 0,94 T : l’imperfection du confinement du champ magnétique dans l’entrefer implique l’existence d’un champ (figure 8) au point où se situe la masse étalon (environ 35 cm au dessus du circuit magnétique, dans son axe de révolution). Ce « champ de fuite », compte tenu de la susceptibilité magnétique volumique de la masse étalon utilisée, induit une force magnétique verticale qui vient s’ajouter à son poids.
Echangeur de masse
Un système (figure 9) a été développé pour apporter la masse jusqu’à la nacelle entre la phase statique et la phase dynamique ainsi que pour la lever et l’abaisser au moment opportun lors de la phase statique : la translation horizontale peut être de 170 mm, et la verticale de 6 mm. Le mouvement horizontal est guidé au moyen d’une glissière commerciale tandis que la linéarité du mouvement vertical est assurée par un pantographe. Pour les deux mouvements, des moteurs piézo-électriques linéaires sont utilisés en boucle fermée à l’aide d’encodeurs linéaires à haute résolution (pas de gravure 10 μm). Le réglage de l’inclinaison de l’échangeur de masse conjugué à la possibilité de réduire la vitesse verticale à une valeur aussi faible que 10 μm/s permettent de réduire au minimum les oscillations de la nacelle de masse lors de la pose et de la dépose de l’étalon. Ce réglage de l’inclinaison consiste à rendre parallèle le plan de la face inférieure du cylindre de la masse étalon placée sur l’échangeur de masse et le plan formé par les trois tiges qui accueillent la masse sur la nacelle.
Poids
Enfin, la connaissance du poids de la masse étalon demande de connaître la valeur de l’accélération de la pesanteur g en son centre de gravité ainsi que la valeur de cette masse. Cette grandeur doit être connue en permanence, la variation quotidienne de g (marées terrestres) étant de quelques 10-7 en valeur relative.
Gravimétrie : accélération de la pesanteur
La valeur absolue de l’accélération de la pesanteur g est tout d’abord mesurée en un point particulier situé dans une
pièce voisine de celle où réside la balance du watt avec un gravimètre absolu reposant sur une expérience d’interférométrie atomique utilisant
des atomes froids de rubidium-87 fonctionnant depuis 2009. Ce gravimètre a été comparé régulièrement avec d’autres gravimètres absolus, en
particulier dans les trois dernières comparaisons clefs (key comparisons). La valeur absolue de g est déterminée par le gravimètre avec
une incertitude-type relative de 4,3×10-9.
Deux opérations supplémentaires sont nécessaires pour transférer cette valeur au centre de gravité de la masse étalon :
— Une cartographie gravimétrique tridimensionnelle du site, combinée avec un modèle du champ gravitationnel des laboratoires permet de
transférer la valeur absolue de g au centre de masse de la masse étalon de la balance du watt. Cette étude a permis, au moyen d’un gravimètre
relatif de type Scintrex CG5, de caractériser l’ensemble du volume des deux salles contigües où sont situées le gravimètre absolu et la balance
du watt et de connaître les variations de l’accélération de la pesanteur avec une incertitude-type relative de l’ordre de 10-9.
— Enfin, l’auto-attraction de la balance elle-même (c’est à dire l’influence des masses qui la composent sur la valeur de g – la contribution la plus
significative étant liée à la présence voisine du circuit magnétique) est prise en compte en utilisant les méthodes développées pour le calcul
de l’auto-attraction du gravimètre absolu: cet effet est déterminé avec une incertitude-type relative de l’ordre de 10-9.
Masse
Les masses étalons de la balance du watt sont raccordées au prototype national français n°35 au moyen du comparateur du LNE de type Mettler M1.
Les contraintes imposées par l’expérience rendent cependant délicate l’utilisation de matériaux traditionnels, en raison en particulier de leur susceptibilité
magnétique.
Pour cette raison, plusieurs études ont été effectuées sur la recherche de nouveaux matériaux. Les critères de sélection
portèrent à la fois sur les aspects mécaniques (dureté, facilité de polissage), magnétiques (faible susceptibilité) et de passivité de surface,
ce dernier point conditionnant le comportement des masses lors du passage air-vide qu’il sera nécessaire de connaître in fine. Les études montrent
que l’iridium pur (et dans une moindre mesure le platine iridié – notamment en raison d’une susceptibilité magnétique plus élevée) est l’un des
matériaux susceptibles de satisfaire à tous ces critères.
Avant que de telles masses ne soient utilisées, un matériau plus classique tel que l’Alacrite XSH a été utilisé dans la campagne de mesure de 2014. Ce
superalliage est composé principalement de cobalt, les éléments restants étant 20 % de chrome, 15 % de tungstène, 10 % de nickel et 0,1 % de carbone.
Sa densité est de 9150 kg/m3 et sa susceptibilité magnétique volumique de 1,34×10-3.
L’étalon de 500 g en Alacrite utilisé lors des mesures de h décrites dans cette thèse a été fourni par la société française Aubert-et-Duval. Cet étalon de
masse a été poli et ajusté au cnam dans les années 1980. Sa stabilité de masse, étudiée pendant des années, est comparable à celle des meilleurs étalons de platine iridié.

Figure 1
Instrumentation autour du dispositif expérimental.

Figure 2
Fléau du comparateur de forces et son capteur optique gaussien.

Figure 3
Position des six capteurs sur la bobine.
Les 3 faisceaux verticaux des interféromètres (faisceaux verts) mesurent les positions (z1, z2 et z3) de 3 coins de cube solidaires de la bobine : on peut alors déterminer
les positions (z, βx et βy) et les vitesses (vz, ωx et ωy ). Les 3 capteurs
gaussiens (faisceaux rouges) mesurent les positions de chacune des 3 lames opaques par rapport à une position de référence propre à chacune de ces lames (d1,
d2 et d3) : on peut alors déterminer les positions (x, y et βz) et les vitesses (vx, vy et vz). Par souci de
visibilité, la mesure d1 n’a pas été représenté. De plus, une lame disposée verticalement près de l’axe de la bobine permet de déclencher les mesures en phase dynamique à une
distance constante du circuit magnétique.

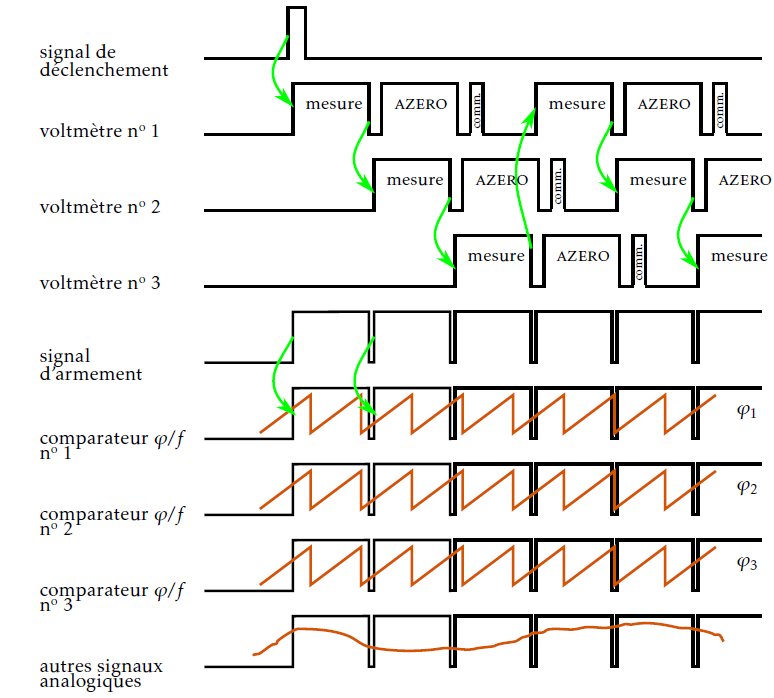
Figure 4
Principe de déclenchement des mesures.
Après le temps de mesure des voltmètres « mesure »), une évaluation de leur tension de décalage interne est effectuée (« azero »), puis un temps
est nécessaire pour les communications (« comm. »). Trois voltmètres sont donc nécessaires pour assurer une mesure quasi-continue de la tension. En phase dynamique,
le passage de la bobine à une position repérée par le capteur gaussien vertical génère l’émission d’un signal de déclenchement.
En phase statique, ce signal est généré par la stabilisation de la position angulaire du fléau du comparateur de force, tel que repéré par un capteur gaussien. Le
premier voltmètre effectue alors une mesure de tension, puis, à la fin de celle-ci, le second voltmètre prend le relais. Une électronique génère un signal
dont les valeurs hautes correspondent aux périodes où les voltmètres effectuaient leurs mesures (« signal d’armement »). Ainsi, les 3 comparateurs phase-fréquence
(« comparateurs Φ/f ») déterminent la position (et la vitesse) de la bobine correspondant à chacune des périodes de mesure. De la même façon, les signaux
analogiques des capteurs de position sont moyennés sur les périodes de mesure des voltmètres.
Mesures de tension et d’intensité
En phase statique, le courant de pesée qui circule dans la bobine est mesuré par la chute de tension qu’il provoque aux bornes d’une résistance R = 200 Ω. Celle-ci,
constituée de deux résistances de 100 Ω en série placées dans une enceinte à air et régulées en température (±10 mK), est étalonnée par comparaison à l’étalon quantique
de résistance.
En phase dynamique, la tension induite est directement mesurée aux bornes de la bobine.
Ces mesures nécessitent de commuter les branchements des voltmètres, de la bobine et de la résistance lors de l’alternance des phases statiques et dynamiques.
Ces modifications sont assurées par des ensembles d’interrupteurs très faibles fem.
Trois voltmètres Agilent 3458A, étalonnés par l’intermédiaire d’une diode Zener, sont utilisés séquentiellement pour déterminer les chute de tensions
aux bornes de la bobine (en phase dynamique) et aux bornes de la résistance étalon (en phase statique).
La référence Zener est elle-même étalonnée périodiquement par comparaison à un étalon Josephson disponible au laboratoire Josephson du lne, distant de quelques dizaines
de mètres.
Asservissement de la position du fléau
Durant la phase statique (pendant les deux équilibres de la double pesée), le courant circulant dans la bobine est ajusté en permanence par un contrôleur temps-réel
comprenant un algorithme proportionnel–dérivé pilotant une source de courant de manière à asservir la position angulaire relative de l’extrémité du fléau supportant la
suspension de masse. Cette source de courant est une source programmable à très faible bruit, et est asservie de façon à assurer l’équilibre du fléau pendant la phase statique.
La détection de la position du fléau est assurée par un capteur gaussien de dynamique 30 μm, solidaire des plateaux mobiles de translation, qui détermine le mouvement
vertical de l’extrémité du fléau. La stabilité du courant en pesée n’est pas limitée par la source de courant, mais sera imposée par les conditions expérimentales et
notamment par le bruit et la dérive du capteur gaussien d’extrémité du fléau.
Mesures de la vitesse et de la position de la bobine
Principe
La bobine (autrement dit le segment inférieur de la suspension) ayant six degrés de liberté, la détermination de ses positions et vitesses nécessite a
minima six capteurs.
Les positions de la bobine dans l’espace sont repérées par les grandeurs x, y et z, tandis que les positions angulaires correspondantes sont ωx, ωy et
ωz. L’axe z est vertical et pointe vers le haut, tandis que l’axe y est dans l’axe du fléau et pointe de la lame centrale vers la lame de
suspension masse. Les vitesses correspondantes sont notées vx, vy, vz, ωx, ωy et enfin ωz.
Trois interféromètres hétérodynes de type Michelson sont utilisés pour déterminer la fréquence Doppler correspondant à la vitesse de trois points régulièrement
répartis sur le pourtour du support de bobine et matérialisés chacun par un réflecteur à coin de cube. Les interféromètres mesurent par intégration de la phase optique à l’aide
d’une carte FPGA et de comparateurs phase-fréquence les positions verticales z1, z2 et z3.
Une transformation matricielle permet d’obtenir la position verticale de la bobine z et ses positions angulaires βx et βy à partir de z1, z2 et z3 ; puis une dérivation permet
ensuite d’obtenir la vitesse verticale de la bobine vz et ses vitesses angulaires ωx et ωy.
Trois capteurs de position sont utilisés pour déterminer les positions d1,
d2 et d3 du bord de lames opaques solidaires de la bobine. Leur principe repose sur les propriétés
de propagation des faisceaux laser gaussiens. Une autre transformation matricielle permet d’obtenir la position de la bobine dans le plan horizontal x et y et sa position
angulaire autour de l’axe vertical βz à partir des informations des capteurs gaussiens d1, d2 et d3 ; puis une dérivation permet ensuite d’obtenir la vitesse de la bobine dans
le plan horizontal vx et vy et sa vitesse angulaire autour de l’axe vertical ωz.
Ainsi, grâce à l’utilisation conjointe des trois interféromètres et des trois capteurs de position, le mouvement de la bobine (positions et vitesses) peut
être connu selon ses six degrés de liberté.
Les informations de vitesse verticale vz en chaque point de la trajectoire x, associée à la mesure de la tension U aux bornes de la bobine permettent
d’obtenir le profil de champ en phase dynamique :
Interféromètres
Les trois interféromètres déterminent la position de la bobine par rapport à la verticale (déplacements verticaux et rotation autour de l’axe vertical) et
donc sa vitesse verticale.
Les interféromètres sont des interféromètres de Michelson hétérodynes éclairés par un laser Nd:YAG commercial (Innolight Prometheus)
doublé en fréquence (20 mW de puissance à 532 nm) et stabilisé sur une raie de fluorescence. Si les faisceaux des interféromètres sont verticaux, le décalage
Doppler νD de l’onde réfléchie par le coin de cube mobile est :
où c = 299792458 m/s est la célérité de la lumière dans le vide, vz la vitesse de déplacement vertical, ν0 la fréquence de l’onde lumineuse dans le
référentiel de la source et nair l’indice de réfraction du milieu de propagation.
La stabilisation s’effectue par l’intermédiaire d’une cellule à fenêtres inclinées contenant du di-iode sous forme gazeuse, refroidie à environ -5°C
(afin de peupler convenablement les niveaux hyperfins de l’état fondamental concerné par la transition optique). Le spectre hyperfin utilisé est celui de la
raie R(56) 32-0, avec comme fréquence de référence la fréquence de la raie a15 (ν0 = 563260509,925 MHz).
La fréquence Doppler correspondant à la vitesse choisie de 2 mm/s est alors de 7515 Hz.
La fréquence hétérodyne est imposée par la différence de fréquences entre deux modulateurs acousto-optiques (pilotés à 80 MHz et 81,5 MHz et utilisés
en double passage). Les bras sont donc séparés en fréquence de 3 MHz. Ces deux faisceaux lasers sont préparés sur une table optique et conduits vers
l’enceinte de l’expérience au moyen de fibres optiques.
Les faisceaux sont séparés au niveau du plateau optique pour alimenter chacun des trois interféromètres placés à l’intérieur de la chambre à vide.
Pour éviter la diaphonie entre les bras de mesure et le bras de référence, les faisceaux se propagent séparément sur une longue distance (plusieurs dizaines
de centimètres) et ne se superposent qu’à la sortie des interféromètres.
Pour réduire autant que possible les effets de dilatation et de vibration du support, pour chaque interféromètre, chacun des deux bras utilise exactement les
mêmes éléments optiques jusqu’à l’interféromètre proprement dit. Pour les même raisons, la distance entre le coin de cube de référence et le coin de cube
mobile est minimisée.
Le faisceau laser de sortie de chacun des interféromètres est collecté par une fibre optique multimode et est acheminé vers la table optique de la salle
instrumentation.
En plus de la mesure de fréquence – et donc de vitesse et de position – proprement dite, les interféromètres ont également pour but d’asservir le
bruit de phase introduit par les fibres.
Synchronisation des mesures de tension et de fréquence
La mesure de tension est réalisée par des voltmètres numériques commerciaux Agilent 3458a, synchronisés sur la fréquence du secteur. Leur temps
d’intégration est ainsi défini par leur propre détermination de cette fréquence de manière à augmenter le taux de réjection des perturbations dues au secteur.
Les voltmètres sont utilisés comme instruments-maîtres pour la synchronisation des mesures et délivrent un signal d’armement ou de déclenchement pour tous les autres
instruments impliqués dans la mesure.
Ils sont configurés en mode auto zéro (« azero ») pour rejeter les tensions de décalages internes : en plus du temps utilisé pour stocker les données dans
la mémoire interne du voltmètre (quelques microsecondes), un autre temps mort de même durée que la mesure de tension est introduit.
Tous ces temps morts pourraient éventuellement être acceptés en phase statique, mais en phase dynamique, ils correspondent à des lacunes dans le
profil de champ. Pour assurer une mesure quasiment continue, il est nécessaire d’utiliser trois voltmètres déclenchés successivement.
Trois voltmètres sont donc utilisés, le second se substituant au premier dès qu’il a terminé sa mesure, puis le troisième au second. Le premier
voltmètre est à nouveau sollicité immédiatement après que le troisième a fini sa mesure. Le déroulement de cette séquence est contrôlé par une électronique
dont les signaux de sorties déclenchent de plus les autres mesures de manière synchrone aux mesures de tension. Ainsi, à chaque portion de la
trajectoire, correspondant à une mesure de tension induite aux bornes de la bobine, est associée une mesure de la fréquence Doppler et donc de la vitesse
de la bobine.
Une électronique dédiée a été développée pour répondre à ce besoin. Son principe est de détecter le signal de fin de mesure d’un voltmètre puis de
déclencher le voltmètre suivant. Ainsi, le signal d’arrêt de mesure du voltmètre 1 déclenche le voltmètre 2, dont le signal d’arrêt déclenche le voltmètre 3,
dont le signal d’arrêt déclenche le voltmètre 1.
Le délai de quelques nanosecondes introduit par l’électronique de déclenchement est négligeable rapporté au délai interne des voltmètres estimé à
moins de 300 ns.
En phase dynamique, l’ensemble des mesures est déclenché par un signal, généré par le passage de la bobine à un point d’altitude fixe (à l’aide d’un
capteur gaussien). Les mesures s’interrompent lorsqu’un signal d’inhibition est envoyé à l’électronique de synchronisation. Ce signal est envoyé en fin de
trajectoire par le même capteur gaussien.
En phase statique, le signal de déclenchement est généré lorsque le bruit d’asservissement de courant du fléau est passé sous un certain seuil. Le signal
d’inhibition est envoyé après une durée choisie.
Un signal d’armement, dont les valeurs hautes correspondent aux périodes où les voltmètres effectuaient leurs mesures, est ensuite utilisé par les trois
comparateurs phase-fréquence (détermination des phases interférométriques), mais également par une carte d’acquisition (qui détermine sur ces signaux
d’armement d’autres grandeurs analogiques nécessaires à la détermination de constante de Planck et en particulier les valeurs des tensions fournies par les
trois capteurs gaussiens périmétriques à la bobine).