Figure 1
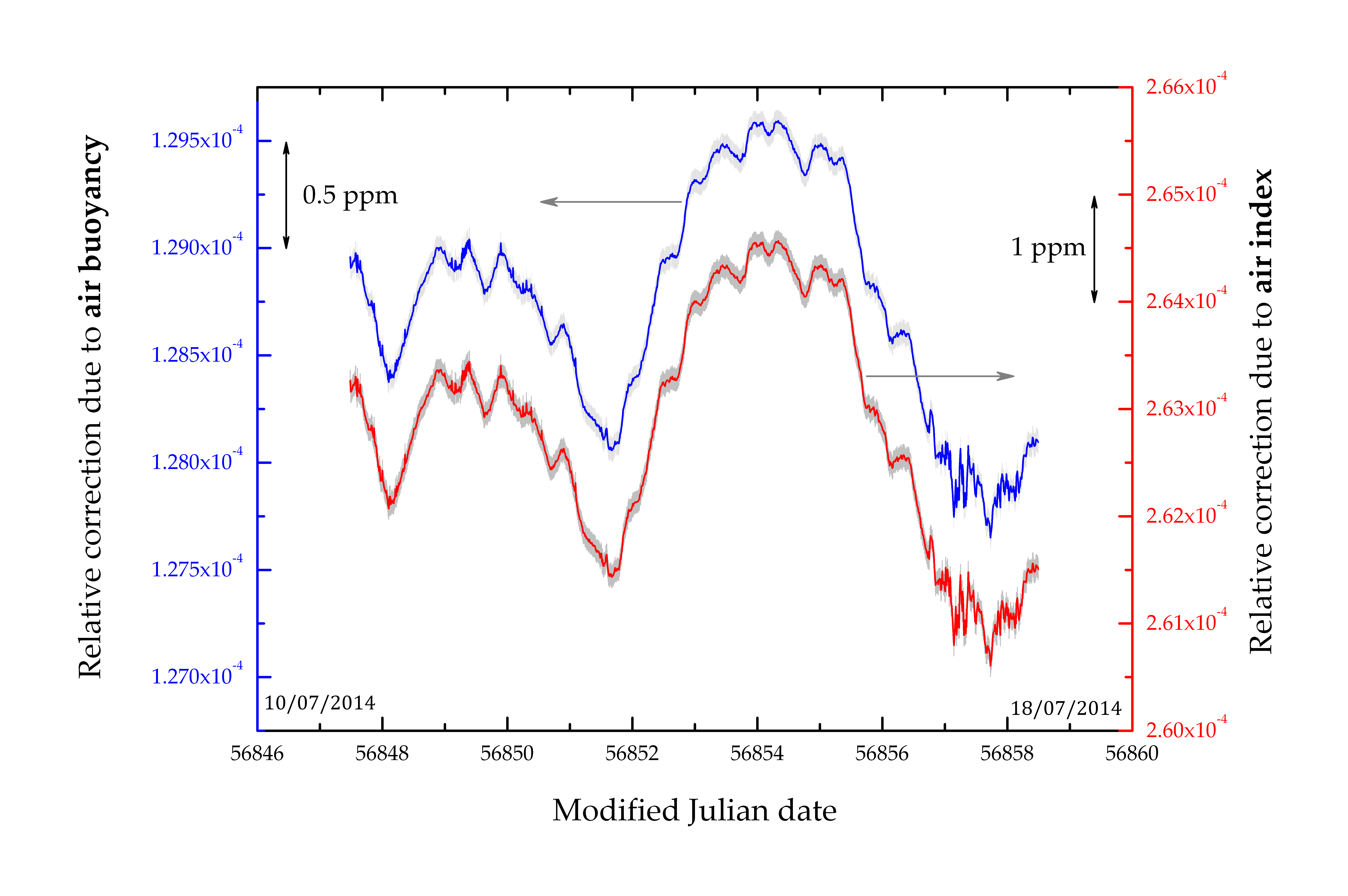
Correction sur la masse m due à la poussée d’Archimède (courbe bleue), correction sur la vitesse vz due à l’indice
de réfraction de l’air (courbe rouge)relativement à la valeur de la constante de Planck. Les surfaces grisées représentent l’incertitude-type combinée
sur ces corrections. Ces valeurs s’étendent sur une durée d’une semaine.
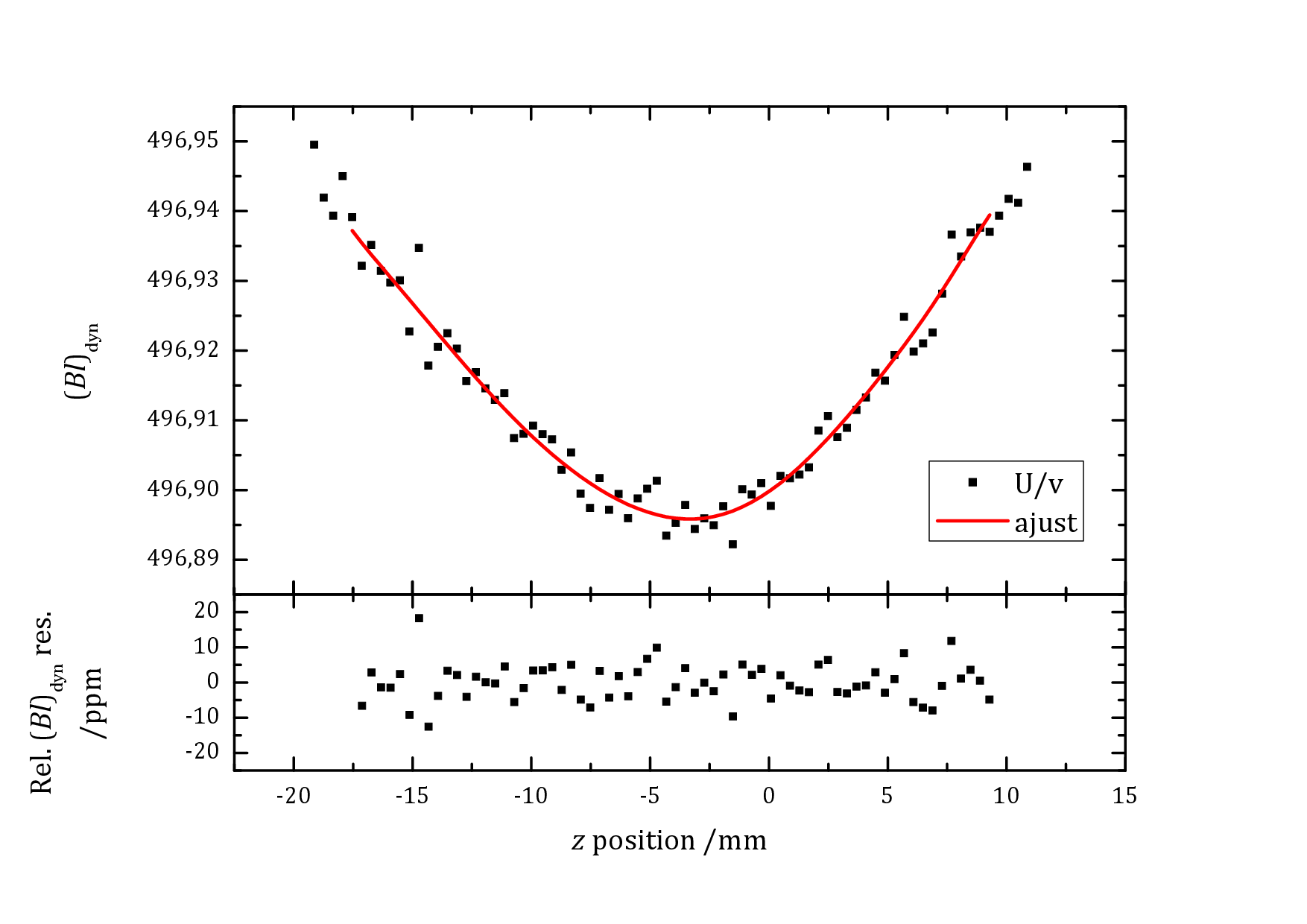
Figure 2
Variation du produit géométrique (B.l)dyn avec la position z.Le produit (B.l)dyn est la
moyenne d'une séquence de 50 montées et descentes. Le trait continu est l'ajustement polynomial utilisé pour estimer la valeur(B.l)dyn
à la position de pesée.

Figure 3
Fléau du comparateur de forces et son capteur optique gaussien.
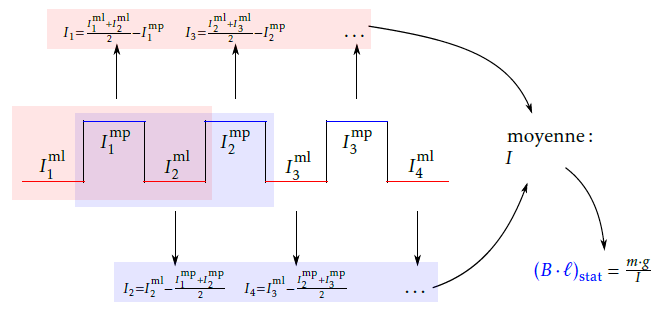
Figure 4
Une séquence de phase statique est composée d’une succession d’équilibres « masse levée »
(courant moyen Iml) et d’équilibres « masse posée » (courant moyen Imp). Le courant de pesée retenu, permettant la détermination
du produit (B.l)stat = m.g/I est la moyenne des différences glissantes des courants.
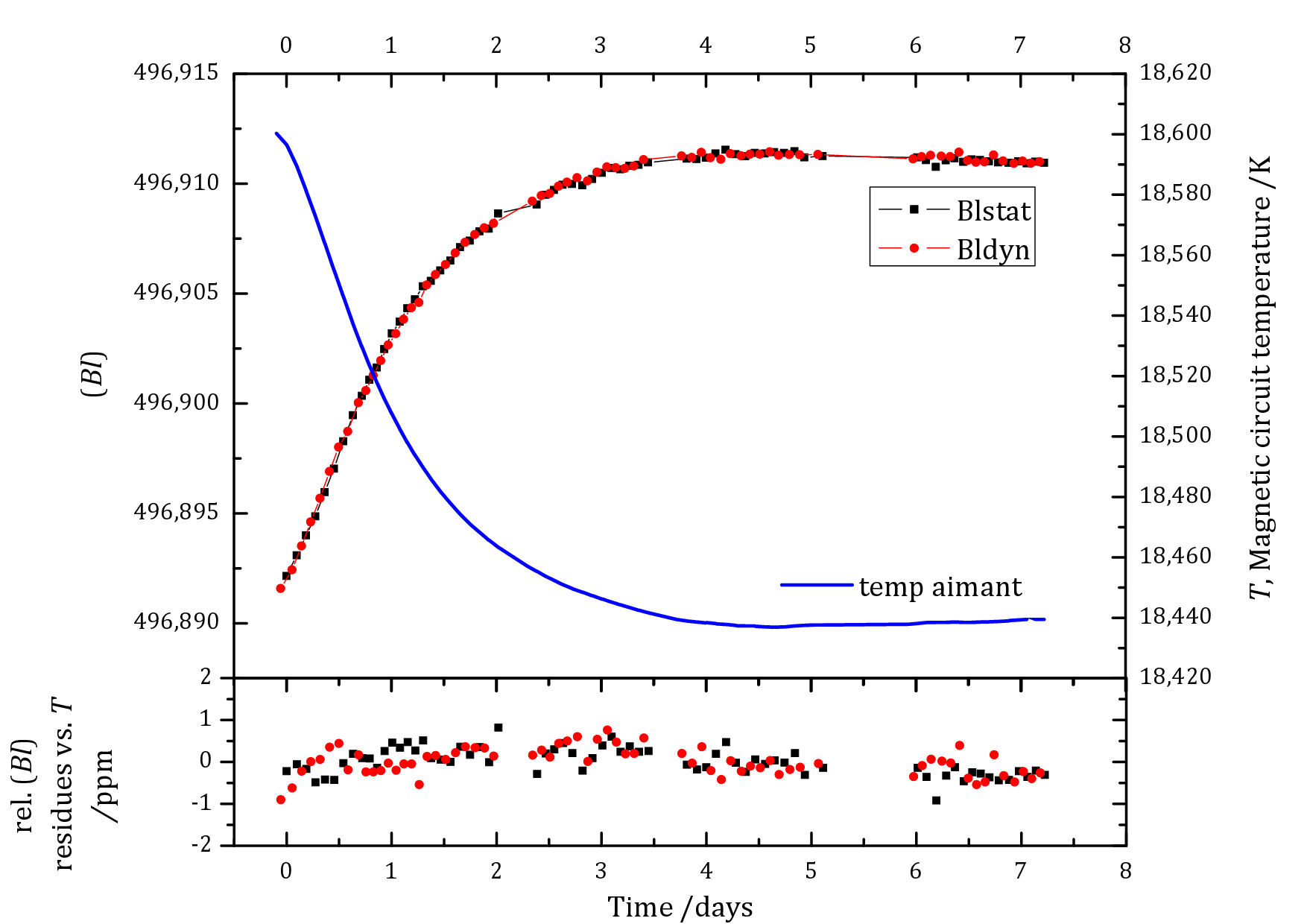
Figure 5
Variations des produits géométriques (B.l)dyn et (B.l)stat sur une semaine. Le trait continu bleu correspond à l'évolution
de la température du circuit magnétique.
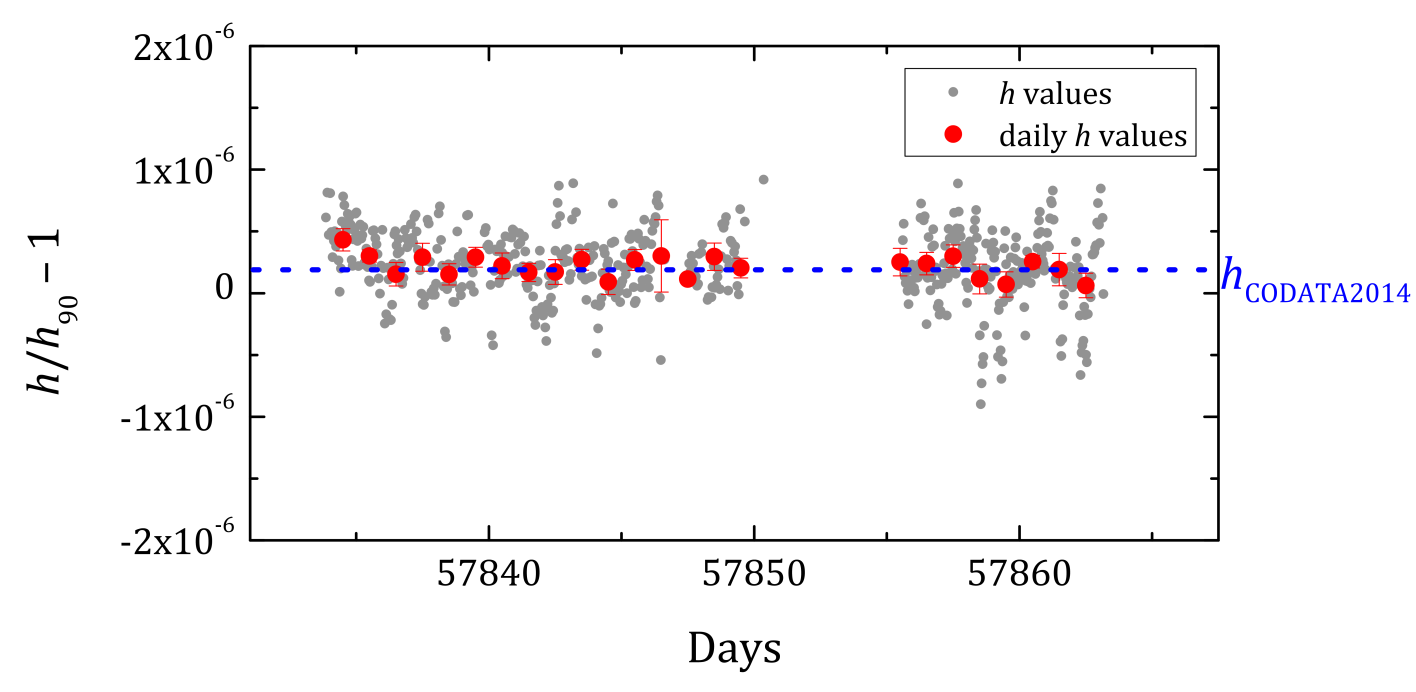
Figure 6
Ensemble des données utilisées pour la détermination de la constante de Planck h.
Chaque point gris représente une détermination de h alors que chaque point rouge représente la valeur moyenne journalière de h et son incertitude
associée.
Les différentes étapes vers h...
Etape 1 : Enregistrement des données environnementales
Toutes les mesures ont été effectuées après que l’enceinte de la balance du watt ait été scellée : la température, la pression,
l’humidité relative et la concentration de dioxyde de carbone ont été mesurées continûment durant les expériences. La masse volumique de l’air
ρair et son indice de réfraction nair ont été calculés à partir des travaux de Ciddòr [1] et des recommandations CIPM-2007 [2].
Ces deux grandeurs sont nécessaires pour calculer la correction sur la masse liée à la poussée d’Archimède et la correction sur la vitesse
liée à l’indice de réfraction de l’air (figure 1).
Etape 2 : Détermination du profil de champ en phase dynamique
La bobine est positionnée au point de départ de la trajectoire. Elle est déplacée vers le bas à une vitesse typique de 2 mm/s, imposée par le moteur
pas-à-pas, sur une distance de 32 mm. Son passage devant un capteur gaussien vertical déclenche puis interrompt les acquisitions de tension et de vitesse.
Durant la trajectoire, la tension Ud, la vitesse vdz (d pour descente)
ainsi que la position verticale z de la bobine sont mesurées et enregistrées simultanément, avec une périodicité de 200 ms,
commandée par les voltmètres. Chacune de ces trajectoires est décrite par 80 points de données et dure 16 secondes.
Le rapport de la tension à la vitesse permet d’obtenir le profil de champ (figure2), soit le facteur géométrique dépendant de l’abscisse
z pour cette première trajectoire :
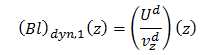
Comme attendu, la forme obtenue pour le profil de champ passe par un minimum (figure2) à mi-hauteur de l’entrefer de l’aimant.
Après la première descente, un déplacement vers le haut est ensuite effectué dans les mêmes conditions. On obtient donc un second profil de champ
(m pour montée) :
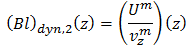
On alterne ainsi les montées et les descentes. Une séquence typique de la phase dynamique consiste en l’enchaînement de cent paires de
trajectoires descendantes et ascendantes de la bobine dans l’entrefer du circuit magnétique. Nous n’avons pas noté de différence significative entre les profils mesurés lors des descentes de la bobine et ceux mesurés lors de ses montées.
Le profil de champ retenu pour cette séquence est la moyenne des profils repérés par l’entier j :
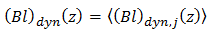
De manière à tirer profit de l’ensemble des valeurs du profil de champ pour la détermination du facteur géométrique à l’altitude z0
de pesée, un ajustement polynomial d’ordre 10 est utilisé sur le profil moyen de champ obtenu et c’est la valeur de ce polynôme en z0 qui
définit le facteur géométrique. L’ajustement permet d’utiliser l’ensemble des informations obtenues lors de la détermination du profil de champ pour
la détermination de (B.l)dyn.
Enfin un certains nombre de grandeurs sont enregistrées durant les trajectoires. En particulier, les vitesses parasites (linéaires et angulaires) de la
bobine sont enregistrées, à partir des informations des capteurs gaussiens de position et des interféromètres.
Etape 3 : Détermination du profil de champ en phase statique
Une séquence de phase statique s’effectue à l’altitude z0. Elle correspond à une succession de paires d’étapes « masses levées » et
« masses posées ».
Pour ces deux étapes, le courant est continûment ajusté par une source programmable de manière à assurer la stabilité de l’angle relatif du
fléau sur l’horizontale (tangage) : le fléau est alors à l’équilibre. La détermination de l’angle du fléau par rapport à un plan nominalement
horizontal est assuré par un faisceau laser focalisé sur une lame solidaire de l’extrémité du fléau (figure 3).
Toutefois, lors de la transition « masse posée » à « masse levée » ou de « masse levée » à « masse posée », la bande passante de
l’asservissement du courant par la source programmable est trop faible pour assurer l’équilibre permanent du fléau : celui-ci s’incline jusqu’à
reposer sur une butée mécanique (inclinaison d’environ 5 mrad) puis retrouve sa position d’équilibre après environ 100 s. À partir de cet instant,
250 mesures de tensions, avec un temps d’intégration de 200 ms, sont effectuées puis moyennées pour obtenir le courant « masse posée »
Imp = Vmp/R , où R la résistance de référence. À l’issue de cette mesure, la masse est élevée de 1 mm
(mesure « masse levée »), à la vitesse de 10 μm/s et le processus est répété pour obtenir Iml = Vml/R.
Cette paire de mesures est typiquement répétée 10 fois (pour une durée d’environ 1 heure), et le courant Ij de pesée est déterminé
(figure 4) comme la différence d’un courant de pesée Imp (respectivement Iml) à la moyenne des courants de pesée adjacents
Iml (respectivement Imp).
Enfin, le courant retenu pour la double pesée est la moyenne des valeurs précédentes :
I=‹Ij(z)›
La connaissance de la masse m, de l’accélération de la pesanteur g et la mesure du courant traversant la bobine lors d’une double pesée
I permet alors d’évaluer le produit (B.l)stat = m.g/I à l’altitude z0.
Etape 4 : Détermination de la valeur de la constante de Planck
Réécrivons l’équation liant la constante de Planck à sa valeur conventionnelle h90 en faisant apparaître les déterminations du facteur
géométrique en phase statique (B.l)stat et en phase dynamique (B.l)dyn :
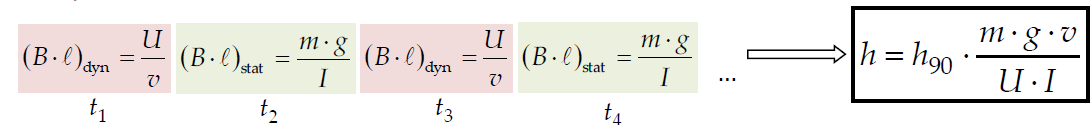
L’alternance des phases dynamique et statique a permis de déterminer les produits (B.l)dyn et (B.l)stat. Du fait de la
dépendance en température des aimants en samarium-cobalt, valant approximativement -3×10-4 K-1, les variations
des valeurs des facteurs géométriques sont corrélées à la température (figure 5).
Comme les phases statiques et dynamiques ne se déroulent pas au même instant (et s’effectuent donc à des températures différentes), la
détermination d’une valeur de h se fait à partir d’une interpolation linéaire des phases successives : on combine une détermination du profil
de champ en phase dynamique (respectivement en phase statique) avec la moyenne de deux déterminations adjacentes du profil de champ en phase
statique (respectivement en phase dynamique).
Ainsi, 270 valeurs de constante de Planck ont été obtenues lors de la campagne 2017. Les résultats sont présentés à la figure 6.
La valeur de h extraite de ces données est:
h = 6,626 070 41(38)×10-34 J.s
Cette valeur diffère en valeur relative de 2,3×10-7 de la valeur de h90 et de 5,5×10-8
de la valeur définie par l'ajustement CODATA 2014 des différentes valeurs de h.
L'incertitude-type relative associée à cette mesure est de:
σh/h = 5,7×10-8
[1] P. E. Ciddór, 1996. « Refractive index of air : new equations for the visible and near infrared », Applied Optics 35:9, pages 1566–1573.
doi :10.1364/AO.35.001566.
[2] A. Picard, R. S. Davis, M. Gläser et K. Fujii, 2008. « Revised formula
for the density of moist air (cipm-2007) », Metrologia 45:2, pages 149–
155. doi : 10.1088/0026-1394/45/2/004.