
Figure 1
Copie du prototype international du kilogramme.

Figure 2
Coffre contenant le prototype international du kilogramme, conservé dans l’air au bipm sous 3 cloches de verre ainsi
que ses 6 copies officielles.
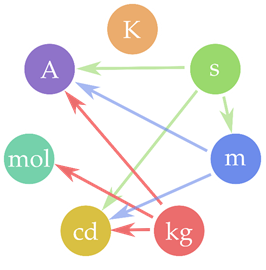
Figure 3
Dépendance des unités du Système International.

Figure 4
Quelle constante fondamentale choisir pour la redéfinition du kilogramme?

Figure 5
Max Planck
Figure 6
Nouvelles définitions des unités.
Vers une nouvelle définition du kg
Raccordement du kilogramme à une constante fondamentale
Problématiques liées à la définition actuelle du kilogramme
La définition et la réalisation du kilogramme sont confondues dans l’artefact ϰ (figures 1 et 2). Cette confusion renvoie à plusieurs problématiques :
- La définition même n’est pas universelle ni dans l’espace, ni dans le temps : il est nécessaire de disposer de ϰ pour réaliser l’unité
de masse et ϰ ne peut être remplacé par un autre prototype (en cas d’usure ou de destruction).
- La maîtrise des conditions de conservation du prototype international du kilogramme est nécessaire pour contrôler sa stabilité à long terme. Ceci
implique de limiter au strict nécessaire l’utilisation du prototype mais aussi de lui appliquer une méthode de nettoyage-lavage « type BIPM » (méthode
utilisant des solvants tels que l’éther et l’éthanol mais aussi de la vapeur d’eau [7,8]) pour éliminer autant que faire se peut les inévitables
contaminations de la surface du prototype international du kilogramme (ainsi que des autres prototypes et étalons de référence en platine iridié)[9].
- L’unicité de référence (sa disponibilité en un seul lieu) rend la vérification des quelques soixante prototypes nationaux possible seulement s’ils
sont tous rassemblés au BIPM pour une durée de deux ou trois années. Ces vérifications « ordinaires » n’ont donc lieu que tous les cinquante ans environ :
distribution et certification des prototypes en 1889 [4], deuxième vérification périodique en 1946-1953 [10], troisième vérification périodique en 1989 [11].
Une vérification extraordinaire a eu lieu en 2014, en prévision de la refonte du SI qui requiert que les masses utilisées comme référence des expériences de
balance du watt ou de sphère de silicium soient raccordées de la manière la plus directe possible au prototype international du kilogramme [13].
Ces vérifications périodiques entre le prototype international du kilogramme et les six témoins conservés dans les mêmes conditions que ϰ montrent des
divergences d’évolution dans le temps (figure 2). La dispersion de l’évolution relative de ces six étalons de masse sur un siècle est de l’ordre de 5×10-8 et
même de 1×10-7 si l’on considère l’ensemble des étalons nationaux. Enfin, la dérive différentielle relative entre les six témoins et ϰ est de
3×10-8: la dérive absolue de masse du prototype international du kilogramme (c’est-à-dire la dérive de la masse de ϰ par rapport
à une hypothétique autre définition de masse), à jamais accessible par définition même, pourrait être plus importante [14,15] : la masse absolue des témoins
(copies chargées de la dissémination du kilogramme) dérive sans doute.
Le fait de voir l’écart de masse entre les six témoins et le prototype international du kilogramme évoluer est un indice fort de l’évolution de la masse
de ϰ par rapport à une référence stable, comme la masse d’une particule. Alors, à prendre la définition de l’unité de masse, on arrive à la conclusion que
la masse du prototype international du kilogramme, m(ϰ), ne varie pas, tandis que la masse d’un électron par exemple dans le SI, varierait au cours des
décennies : cela est a minima insatisfaisant. Par ailleurs, la tendance à l’accroissement de masse des copies officielles (relativement à ϰ) observée durant
les trois premières vérifications (1889, 1946, 1988-1992) n’a pas été confirmée par la dernière vérification : ces résultats montrent que la différence de
masse entre ϰ et ses copies officielles n’a changé en moyenne que de 1 µg : la dérive des copies par rapport à ϰ n’est pas prévisible.
En sus de l’arrêt de la dérive observée précédemment, l’unité de masse maintenue au BIPM depuis la troisième vérification à partir d’une dizaine de
kilogrammes en platine iridié a été déterminée comme erronée de 35 µg [16] relativement à la masse de ϰ (soit 3,5×10-8 en valeur
relative). L’évolution de ce décalage dans le temps (de 1992 à 2014) a été modélisée en supposant une diminution de masse des prototypes proportionnelle
au nombre de pesées dans les comparateurs de masse. Les corrections sur les valeurs des étalons nationaux ont été calculées a posteriori. L’incertitude-type
associée a été déterminée à 3 µg et l’ensemble de ces informations transmises aux instituts nationaux de métrologie (INM) à la fin 2014 : l’unicité de la
réalisation du kilogramme rend les erreurs difficiles à détecter, puisque des intercomparaisons entre réalisations primaires ne sont pas possibles.
Cette situation problématique dans le domaine des masses l’est également pour les unités qui en dépendent : la mole, la candela et surtout
l’ampère [17,18,19] et donc, par extension, l’ensemble des unités électriques. En effet, bien que les grandeurs de base soient, par convention, considérées
comme indépendantes, l’examen de leur définition montre que certaines d’entre elles sont liées (figure 3). C’est en particulier le cas de l’ampère dont la
définition fait intervenir une force s’exprimant elle-même en fonction du mètre, du kilogramme et de la seconde : les faiblesses de la définition du
kilogramme se répercutent sur d’autres unités du SI.
Pour des raisons de disponibilité, de pérennité et d’universalité du kilogramme (et des unités qui en dépendent), il est donc indispensable d’en changer
la définition actuelle basée sur un artefact matériel unique. Cet artefact, de masse constante par convention, est en réalité physiquement variable du fait
des effets de l’usure, du dégazage et de la contamination superficielle et il est impossible à copier à l’identique, c'est-à-dire au microgramme près en
termes de masse.
Raccordement du kilogramme à une constante fondamentale
Quelle constante fondamentale choisir pour le kilogramme?
Des principes physiques variés, comme le « comptage » d’ions pour former une masse d’atomes d’une dizaine de grammes [20] ou encore la lévitation d’une masse supraconductrice [21,22] ont été envisagés pour établir le lien entre le kilogramme et une ou plusieurs constantes fondamentales de la physique. Après des réflexions sur les nouvelles définitions, et sur le choix des constantes qu’il serait le plus pertinent de fixer (figure 4) [23,24,25], et bien qu’une définition fondée sur la constante d’Avogadro NA [26] – selon laquelle le kilogramme serait constitué d’un nombre donné d’atomes – soit conceptuellement simple, un consensus s’est dégagé pour déterminer le kilogramme à partir de la valeur de la constante de Planck [27] (figure 5) pour les raisons suivantes:
- La constante de Planck h fait partie des « trois constantes dimensionnées les plus fondamentales » de la physique [28] avec la vitesse de la lumière c et la constante de
gravitation G.
- Fixer h indépendamment de NA permet de définir la mole comme une quantité de matière, grandeur indépendante de la masse ;
- Enfin, fixer la valeur de la constante de Planck h et la valeur de la charge élémentaire e implique [23] que la constante de Josephson KJ et la constante de von Klitzing RK
auront des valeurs exactes dans le SI, considérant la validité des expressions théoriques : KJ = 2e/h et RK = h/e2.
La modification de la définition du kilogramme s’inscrirait alors dans une redéfinition globale des unités du SI, permettant d’élaborer un système d’unités reposant entièrement sur des constantes fondamentales
.Nouvelle définition du kilogramme
Dans un premier temps, il s’agirait d’effectuer des déterminations de la constante de Planck dans le SI actuel (et donc avec la masse du prototype international du kilogramme
exactement égale à 1 kg) au moyen de balances du watt ou de sphères de monocristal de silicium isotopiquement pur (utilisant une méthode dite X-ray-crystal-density), les expériences
les plus prometteuses en termes d’incertitudes.
Puis, une fois la robustesse de ces différentes déterminations établies (cohérence, incertitude), d’inverser le sens de l’expérience
et de déterminer une masse (par exemple celle du prototype international du kilogramme, mais plus vraisemblablement de tout autre étalon de masse) en se donnant
une valeur fixe de la constante de Planck.
On effectuerait alors une « réalisation primaire » de l’unité de masse (par les balances du watt ou les sphères de silicium), point de départ de la
dissémination de l’unité de masse aux utilisateurs (« mise en pratique de la définition du kilogramme»).
La 24ème CGPM [29] en 2011 propose selon ce principe une nouvelle définition à constante explicite pour le kilogramme (mais avec pour l’instant une valeur
à préciser pour la constante de Planck), de même que pour les autres unités de base, et cela dans le cadre d’une refonte globale des définitions des unités de
base du SI, définies également à constantes explicites [27] :« Le kilogramme, symbole kg, est l’unité de masse ; son amplitude est déterminée en fixant la
valeur numérique de la constante de Planck à exactement 6,62606…×10-34 lorsqu’elle est exprimée en m².kg.s-1, unité du SI égale au joule seconde, J.s. »
Cependant, lors de sa 25e session en 2014, l’assemblée constate que « malgré les progrès effectués [dans les déterminations de h], les données disponibles ne semblent pas
encore suffisamment robustes pour que la CGPM adopte le SI révisé [et donc la nouvelle définition du kilogramme] » [30]. En effet, les conditions sur les valeurs de la
constante de Planck exigées par le Comité international des poids et mesure (CIPM) avant de procéder à une redéfinition du kilogramme s’appuyant sur une valeur de h,
sont notamment que trois expériences indépendantes (incluant des balances du watt [31] et des expériences de sphère de silicium [32]), permettent d’obtenir des valeurs
cohérentes de la constante de Planck, avec des incertitudes-types relatives qui ne soient pas supérieures à 5×10-8 et dont l’une au moins
possèderait une incertitude-type relative qui ne soit pas supérieure à 2×10-8 [13].
Une telle exigence sur les niveaux d’incertitude est en effet le seul moyen de garantir la continuité historique de la valeur du kilogramme (conservation de sa magnitude lors
des redéfinitions successives), de même qu’elle est le seul moyen pour que cette définition n’entraîne pas d’écart significatif sur les valeurs de masse conventionnelle des
poids et masses-étalons de la classe d’exactitude la plus élevée (E1) définie selon la recommandation R111 de l’Organisation internationale de métrologie légale (OIML):
autrement dit, il est nécessaire de pouvoir étalonner des masses de 1 kg en acier inoxydable avec une incertitude-type relative inférieure à 8×10-8
[33], cela sous-entend de maîtriser l’étalonnage de masse en platine iridié à 5×10-8 ou mieux.
La redéfinition est donc finalement prévue pour 2018...